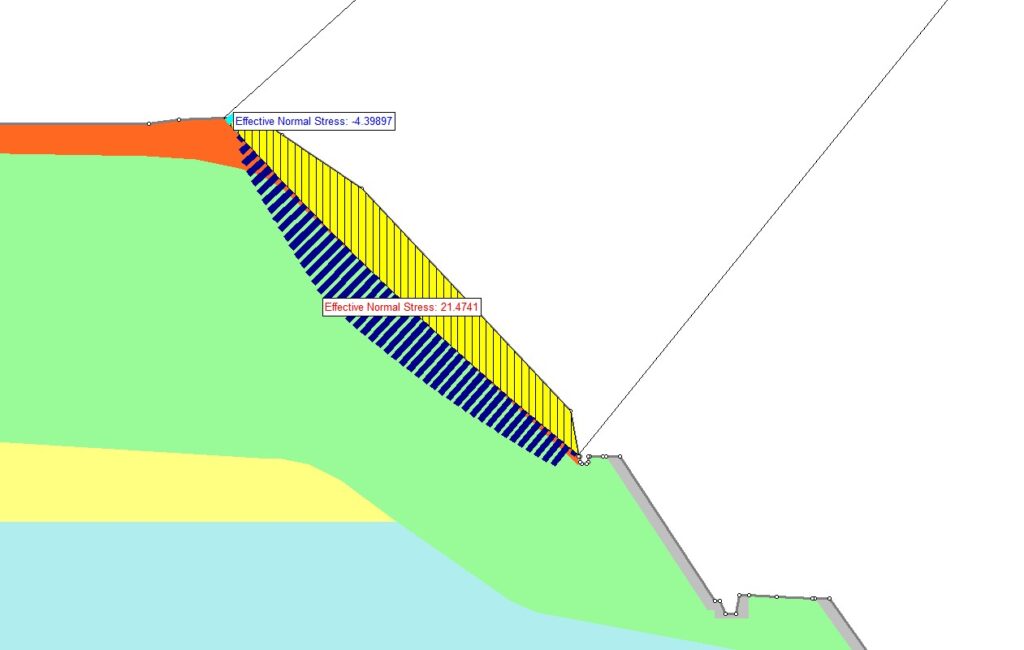
前回、すべり面に垂直に働いて移動土塊をすべり面に押さえつける応力(下図紺色)と、すべり面のせん断強さ(下図赤色)を視覚的に確認しました。すべり円弧の移動土塊をスライスに分割することで、各スライスに働く応力とせん断強さを表示しました。
さて今回は鉄筋挿入工として、ここにロックボルトを入れて斜面を補強してみます。
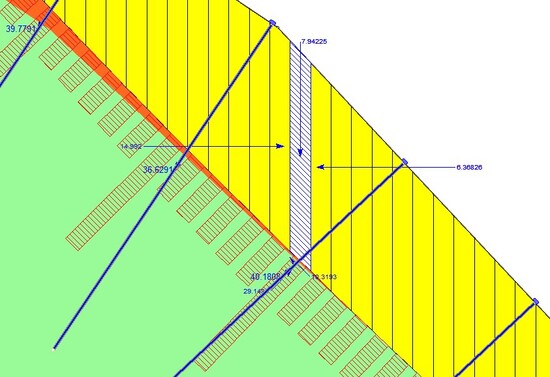
ロックボルトを設置するとすべり面に働く垂直応力は、下記のように変化します。
(※ロックボルトがあるほうが、紺色のバーが全体的に短くなっていますが、バーの単位長さ当りの値の大きさが異なるので、ロックボルトが無い場合とある場合でバーの長さでは単純比較できません。せん断強さにおいても同様です)
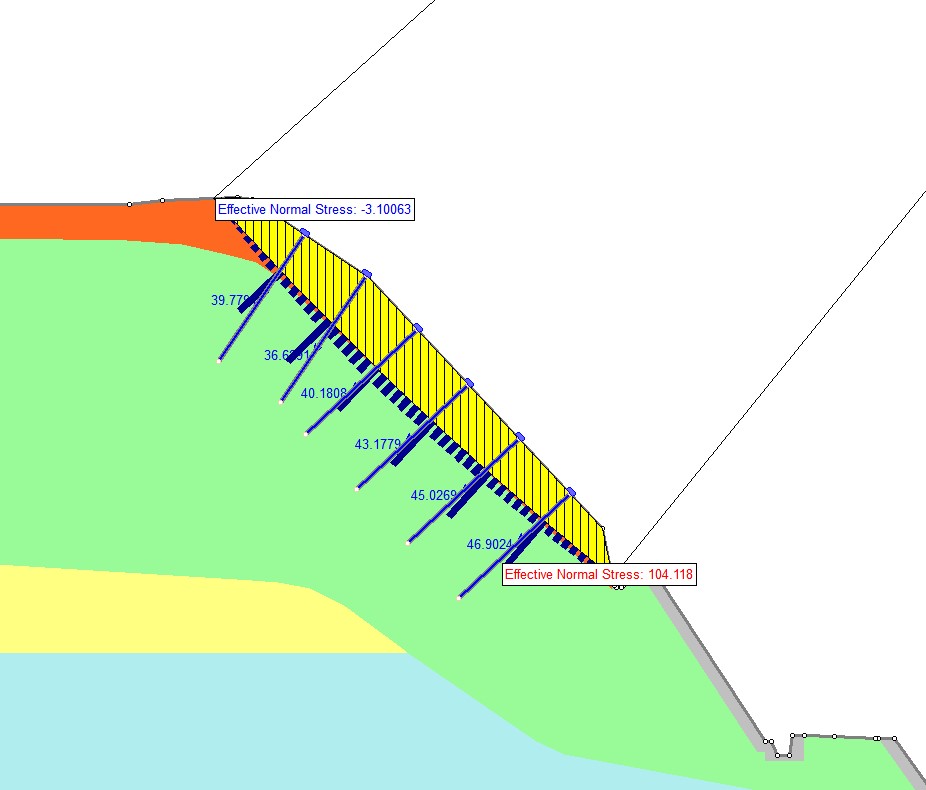
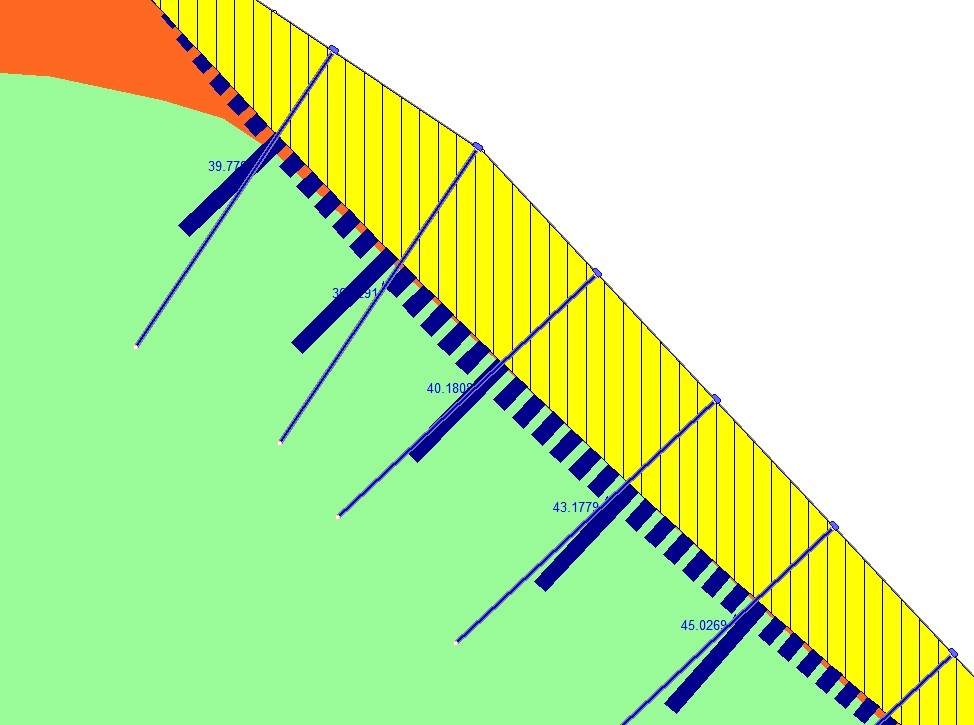
ロックボルトが交差するスライス底面をご覧ください。垂直応力を示すバーがほかに比べて極端に突出していることがわかります。
これがいわゆるロックボルトの締め付け効果です。
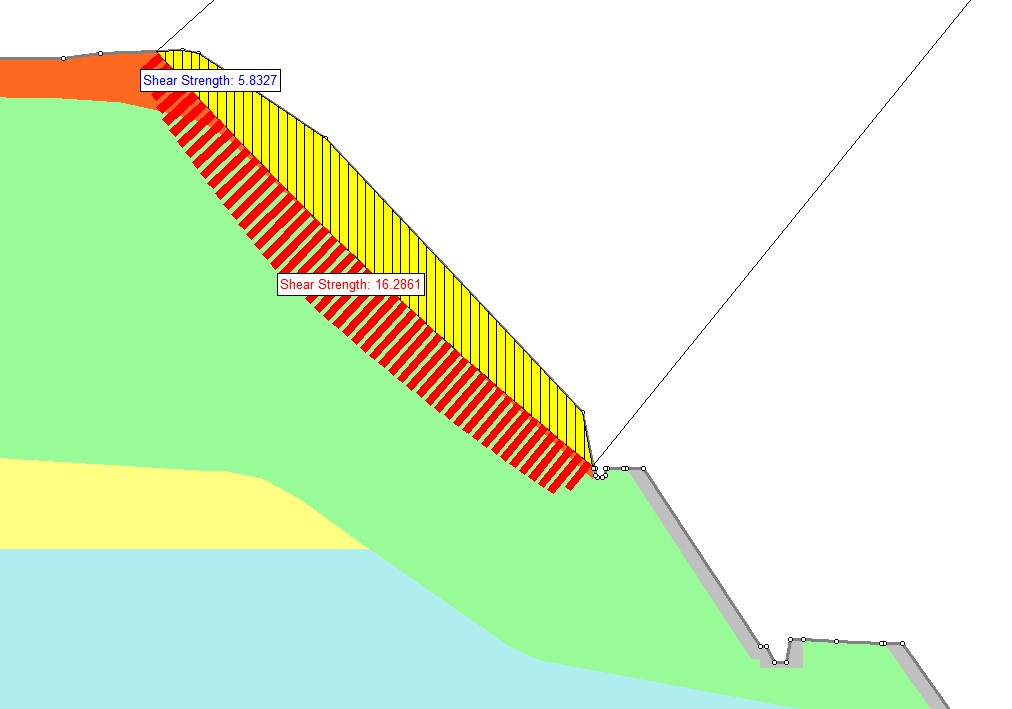
続いて、上記を考慮したすべり面のせん断強さがロックボルトを設置したことでどう変化したのかみてみます。
クーロンの式からわかるように、せん断強さはすべり面の底面に働く垂直応力の大きさに比例するので、これにすべり面に平行な引き止め効果を加わってロックボルトが交差するスライスのせん断強さが大きくなっています。
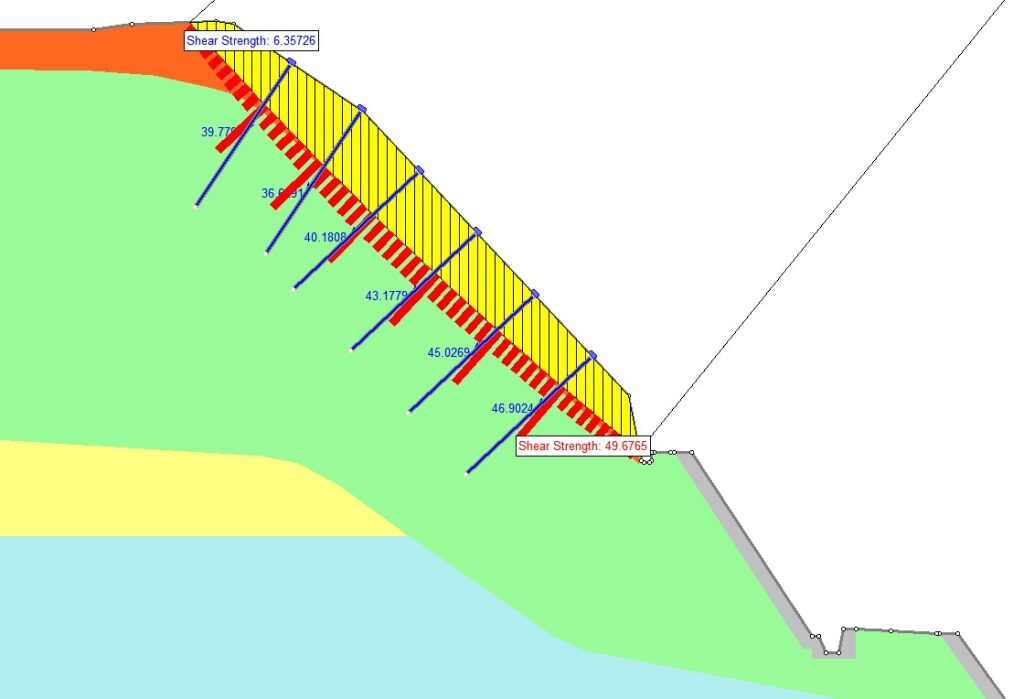
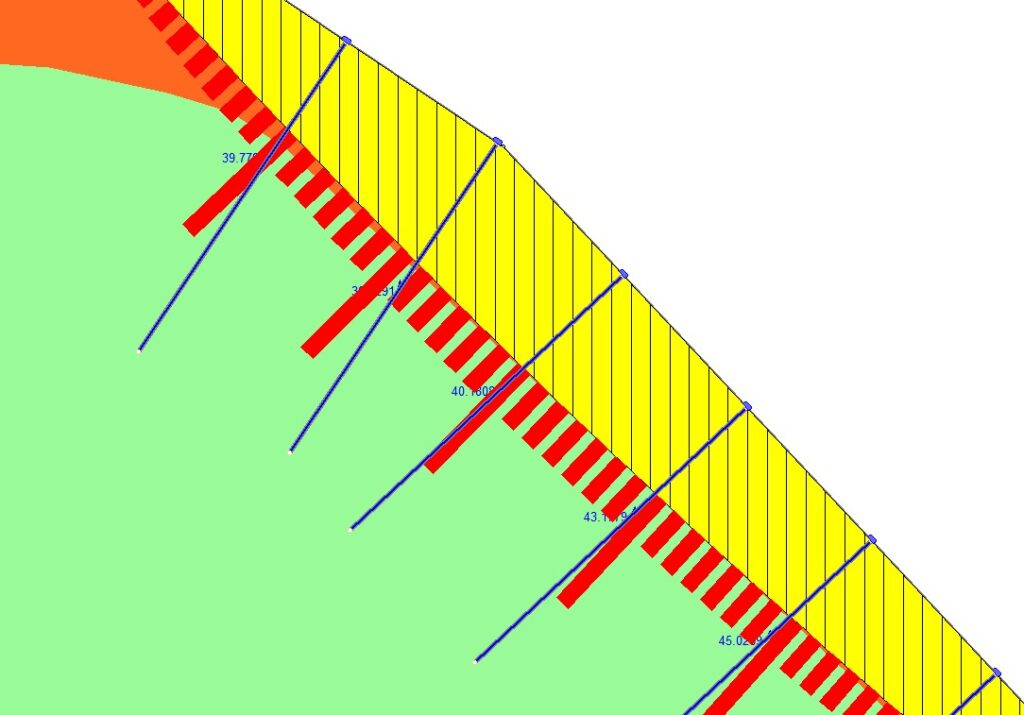
ロックボルトの効果は、ロックボルトが交差するスライス底面のせん断強さをモーメントとして合計することで、すべり面トータルのせん断強さを計算することができます。
では、ロックボルトがすべり円弧の内側に収まっている場合、斜面補強効果があるのか見ていきます。
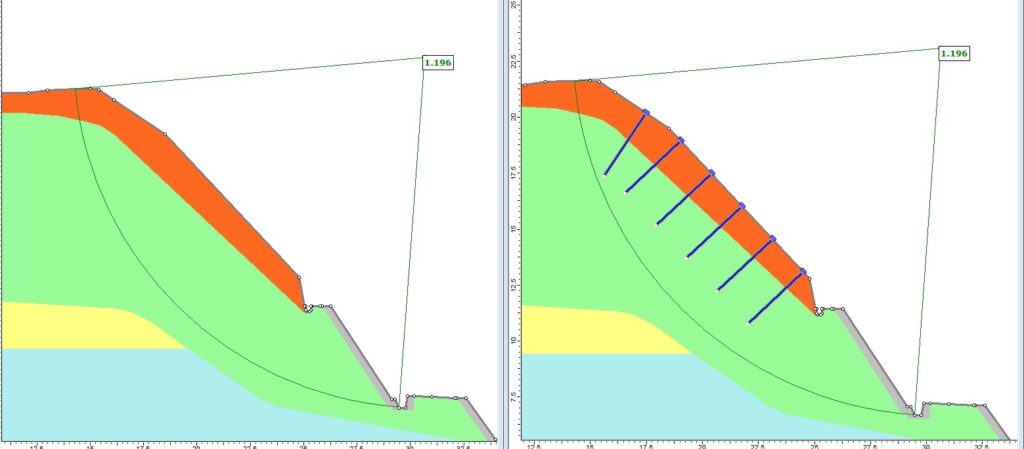
下記図の左は、無補強の斜面の安定解析結果です。このすべり円弧を指定した場合、この斜面の安全率(Fs)は、1.196です。
右は、すべり円弧に交差していないロックボルトを挿入して同じ円弧で補強後の安定計算した結果です。字が小さくて見にくいですが、安全率は同じく1.196です。
ロックボルトを一生懸命6本配置しても計算上、このすべり面を抑止する効果は何もないことがわかります。無数に発生する円弧のうち、このすべり面より浅い円弧(たとえば上の図の円弧)に対しては効果があるので、もちろんやらないよりはましです。
しかし、このすべり円弧に対しては何の効果もないので、安全率が1.196以上より大きくなることはありません。
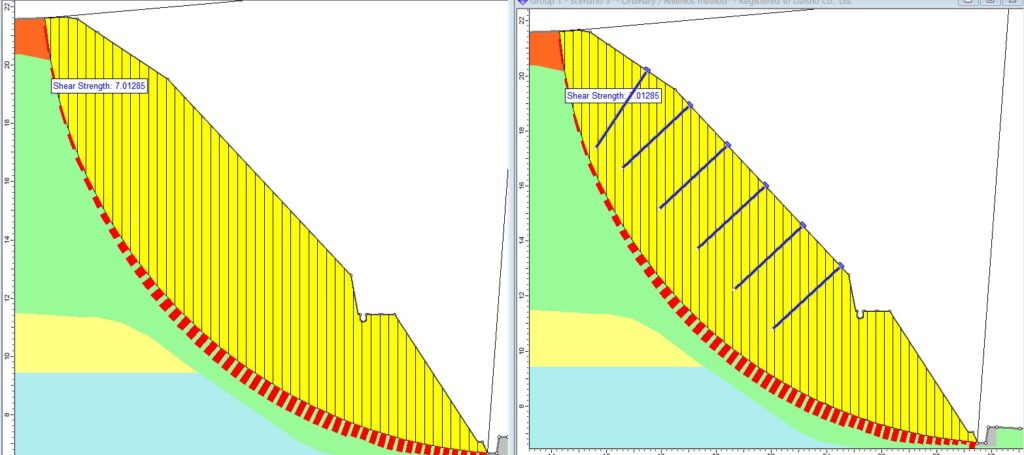
斜面の安全率が何も変わっていないことからもわかる通り、ロックボルトを入れても指定したすべり面のせん断強さはなにも変わっていないことが下の図から確認できます。
ロックボルトは全面定着なのでグラウンドアンカーのように岩着とか定着層がまだ現れないとか難しいことは考えなくてもよいですが、それは決してすべり面と交差しなくてよいことを意味しないことが視覚的に理解できました。
以上、当たり前のことですけれど、1つずつ確認していきました。
すべり円弧の各スライス底面に作用する応力の大きさを可視化することで、すべり円弧と補強材のなす角度が、補強材の効果(締め付け効果・引き止め効果)に大きく影響しそうなことも想像できます。
出来形管理などの施工管理では補強材の打設角度は法面直角などと決まっていて管理することはあっても、すべり面と補強材がなす角度については設計照査や安定計算の段階が過ぎればとくに考えることがありません。
これも当たり前ですが、大事なのはすべり面と補強材の角度なので、これがロックボルトの補強力にどんな効果を与えるかまた考えていきたいです。