さて、せん断される土へ設置される補強材の引張力の効果が最大限に発揮されるのは、最小主応力方向に配置されるときでした。
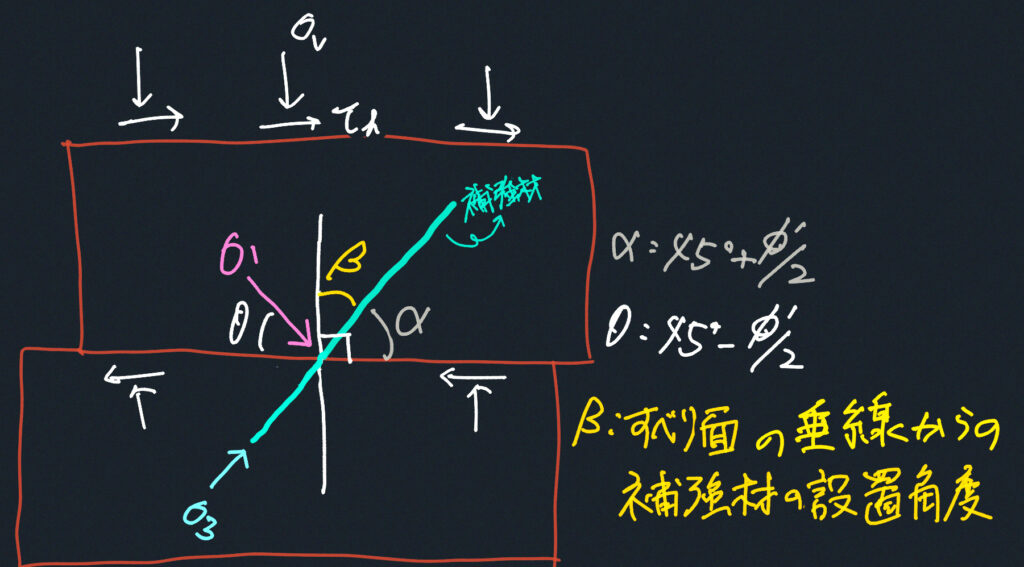
その角度は、β=30°前後となります。つまり、すべり面の垂線から30°程度寝かせた角度となります。
その時、のり面と補強材の交差する角度は、のり面(地表面)の勾配や形状によります。それでもとくに法枠の現場など、施工性を優先したのり面直角のケースが多いのは、最小主応力方向の±15°くらいではあれば最大値に比べて引張力が大きく減少しないことがわかっているからです。
では、この問題について考えるにあたって、まず斜面地盤内のすべり面に働く主応力の状態をみていきます。主応力とは、地盤内のある成分を取り出したときに、せん断応力が0となる面に垂直に働く応力です。2次元では、最大主応力σ1と、最小主応力σ3の2つの主応力が存在します。
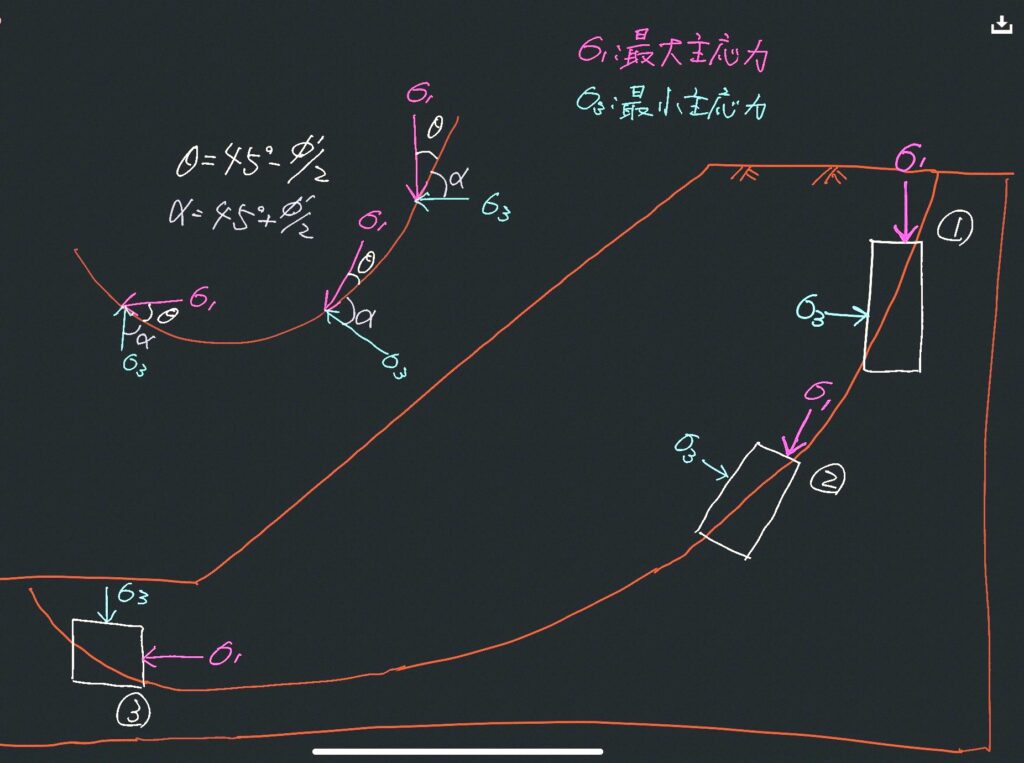
そして、補強材の力が最大に発揮されるのは最小主応力方向でした。つまり、上の図の水色のσ3方向となります。
すべり円弧の上のほうでは、最大主応力σ1はほぼ鉛直、最小主応力σ3はほぼ水平に働きます。つまり、擁壁の土圧を検討するときなどに考慮する主働土圧と同じです。
すべり円弧の方向に従って、σ1の方向も傾いていきます。
おもしろいのは、斜面の法尻、地盤の底部のほうではσ1は水平方向に近く、σ3が鉛直方向に近くなるので、最終的には受働土圧状態になることです。
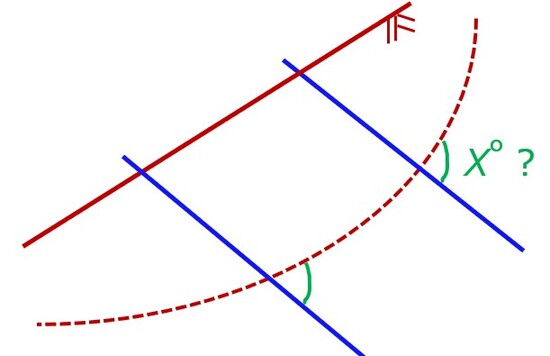
図のθ=45°-φ/2やα=45°+φ/2は、お馴染みの角度ですよね(φは、もちろん土の摩擦角です)。
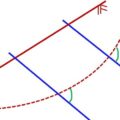
図を見てもらうとわかりますが、最大主応力方向とすべり面がなす角度θは常に、45°-φ/2です。
主応力は直交するので、すべり面から45°+φ/2寝かせたのが最小主応力方向、つまり補強材に引張力が最も働く角度になります。
すべり面からの角度といってもすべり面は円弧だからと一瞬難しそうに思いますが、すべり面をスライスに分割することで、円弧を微分するように限りなく直線として扱いやすくしています。そのスライス底面の直線からの角度で求めることができます。
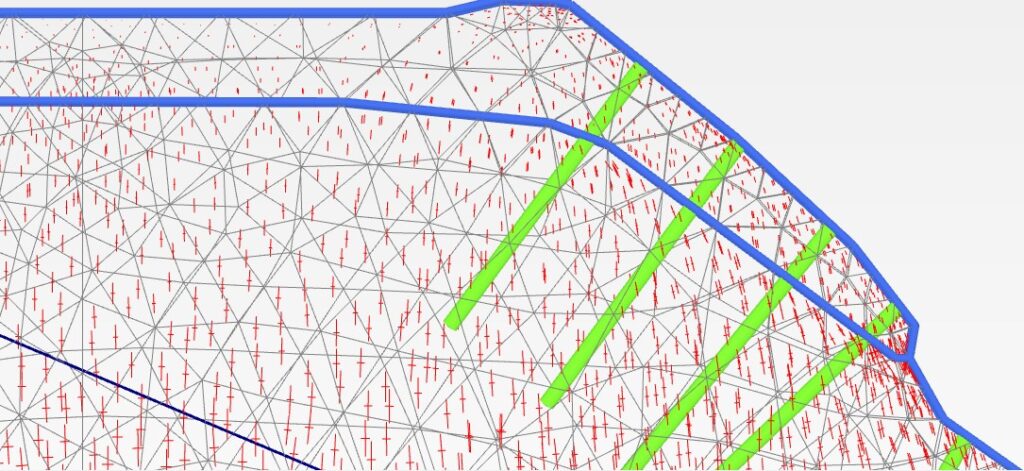
ちなみに余談ですが、上の図のイラストで描いた地盤内の主応力σ1,σ3の方向や最小主ひずみε3方向は、下記の通り斜面地盤をFEM解析することで覗き見ることができます。
まず、主応力から。
主応力はそれぞれ直角に働くので、最大主応力σ1と最小主応力σ3は十字で表現されます。
長いほうがσ1、短いほうがσ3となります。
主応力の向きがイラスト同様に天端から法尻にかけて変化していくのがわかるでしょうか。
σ1が鉛直方向だったのが、斜めに傾いていき、最後はσ1が水平方向に近くなっています。
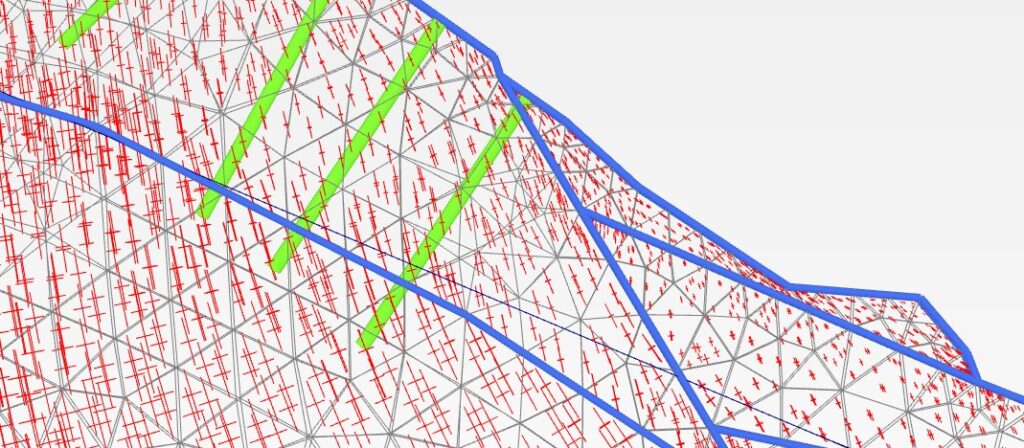
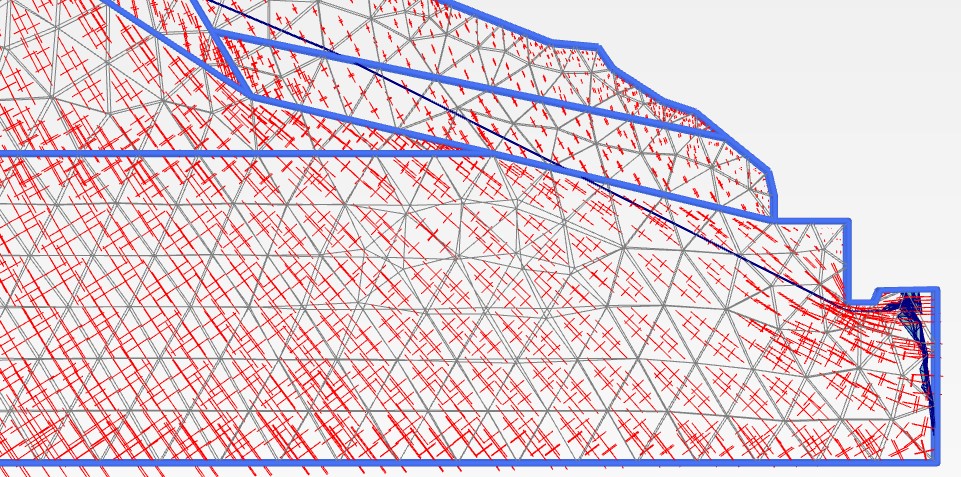
続いて、切土補強土工指針の図に出てくる最小主ひずみ(最大伸長ひずみ)ε3方向を下記に表現します。
最小主ひずみ方向は、最小主応力の主方向と同じです。
下のε3の方向に近ければ近いほど、補強材は引張材としてよく機能するということです。

これまでを踏まえると、下記の図が腑に落ちるかと思います(図の中のα、βの使い方は異なります)。
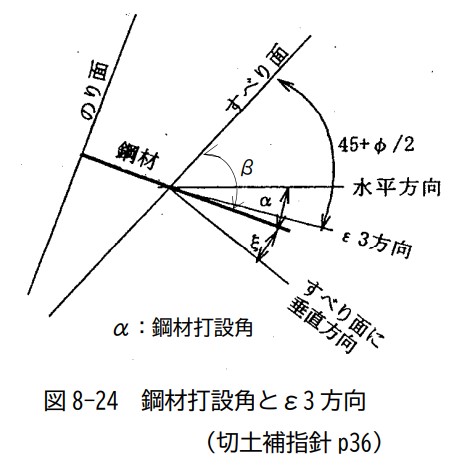
さて、上記を踏まえて実際に斜面に最小主応力方向に補強材を配置してみます。
すべり面と補強材の角度だけを考えると、のり面では補強材がまちまちな角度となるので、実際の施工ではのり面直角や角度指定となることがよく理解できます。土質によるようですが、少なくともβの±15°であれば効果は大きく低減されないので、効果と施工性を考慮することができるのでした。
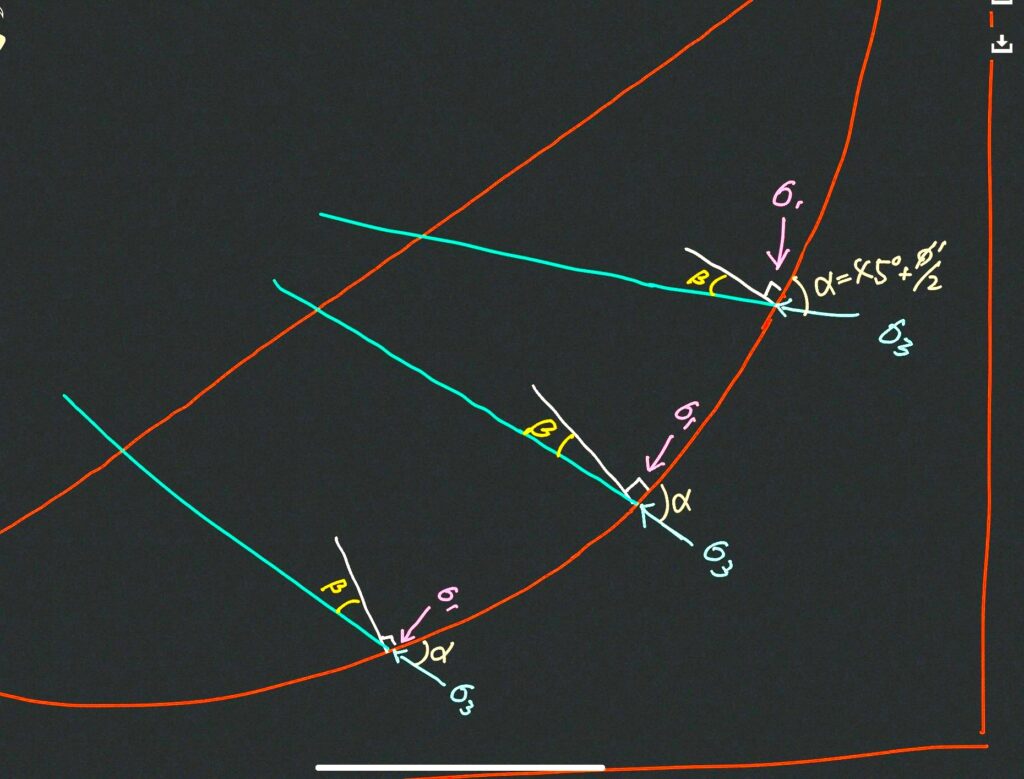
ちなみに、βが実験から30°くらいになる理由も図を見れば大体わかります。
土の摩擦角は、たいてい30°前後なので、β = 90°-(45+30/2) = 30となり、30°前後となるわけです。
さて以上から、補強材を効果的に設置するための角度はわかりました。
ところで、仮に上記の斜面を法枠で補強して補強材の角度がのり面直角だとどうなるか想像してみてください。
下2段の補強材に対して、最上段の補強材は、すべり面と垂直な白い線より立つことになりますよね。のり面直角の現場では、すべり面とこういう角度で交差していることがよくあります。
次回は、そんなときにどんなデメリットがあるのか、考えていきます。
少し長くなってしまいました。引き続きお楽しみに^^